Working with matrixes
- Goals
- Imports
- Matrix mutliplication
- Reshaping Matrixes
- One-hot encoding
- Squaring, log, square root
- Manipulating
tf.Variabletensors - Tensors and NumPy
- Using
@tf.function - Checking access to GPUs
- Matrix Practice# Tensorflow: Working With Matries
Goals
An Overview of working with matrixes, tensorflow, and numpy.Imports
import datetime
import numpy as np
import tensorflow as tf
print(f'tensorlfow version: {tf.__version__}') # find the version number (should be 2.x+)Working With Matrixes
Matrix mutliplication
> 🔑 Note: '@' in Python is the symbol for matrix multiplication.
One of the most common operations in machine learning algorithms is matrix multiplication.
TensorFlow implements this matrix multiplication functionality in the tf.matmul() method.
Matrix Multiplication Rules
The inner dimensions of the two matrixes must match:-
(3, 5) @ (3, 5)NOPE! -
(5, 3) @ (3, 5) -
(3, 5) @ (5, 3)
- The resulting matrix has the shape of the outer dimensions:
(5, 3) @ (3, 5)->(5, 5)(3, 5) @ (5, 3)->(3, 3)
simpleTensor = tf.constant([[10, 7], [3, 4]])
# Matrix multiplication in TensorFlow
tensor = tf.constant([[[1, 2, 3],
[4, 5, 6]],
[[7, 8, 9],
[10, 11, 12]],
[[13, 14, 15],
[16, 17, 18]]])
print('TENSOR--------')
print(tensor)
print('----tensor MULTIPLIED----')
tf.matmul(simpleTensor, simpleTensor)# Matrix multiplication with Python operator '@'
simpleTensor @ simpleTensor# Create (3, 2) tensor
X = tf.constant([[1, 2],
[3, 4],
[5, 6]])
# Create another (3, 2) tensor
Y = tf.constant([[7, 8],
[9, 10],
[11, 12]])
X, Y#
# Will ERROR
#
# X @ Y
# will return
# InvalidArgumentError: {{function_node __wrapped__MatMul_device_/job:localhost/replica:0/task:0/device:CPU:0}} Matrix size-incompatible: In[0]: [3,2], In[1]: [3,2] [Op:MatMul]Trying to matrix multiply two tensors with the shape (3, 2) errors because the inner dimensions don't match.
We need to either:
- Reshape X to
(2, 3)so it's(2, 3) @ (3, 2). - Reshape Y to
(3, 2)so it's(3, 2) @ (2, 3).
Reshaping Matrixes
Reshaping can be done with either:tf.reshape()- reshape a tensor into a defined shapetf.transpose()- changes the dimensions of a given tensor
Reshape
# Example of reshape (3, 2) -> (2, 3)
print('-----Y----')
print(Y)
print('-----Y reshaped----')
tf.reshape(Y, shape=(2, 3))#
# NOW multiplying X & Y works
#
X @ tf.reshape(Y, shape=(2, 3))# Example of transpose (3, 2) -> (2, 3)
tf.transpose(X)#
# NOW multiplying X & Y will work
#
tf.matmul(tf.transpose(X), Y)tf.matmul(a=X, b=Y, transpose_a=True, transpose_b=False)Notice the difference in the resulting shapes when tranposing X or reshaping Y.
Machine-Learning Engineers & those working in neural-networks may spend a bunch of time reshaping data (in the form of tensors) to prepare it to be used with various operations (such as feeding it to a model).
The dot product
Multiplying matrices by eachother is also referred to as the dot product.tensordot
You can perform thetf.matmul() operation using tf.tensordot().# Perform the dot product on X and Y (requires X to be transposed)
tf.tensordot(tf.transpose(X), Y, axes=1)Comparing reshape & transpose
These two get different results.#
# transposing Y
#
# Perform matrix multiplication between X and Y (transposed)
tf.matmul(X, tf.transpose(Y))#
# reshaping Y
#
tf.matmul(X, tf.reshape(Y, (2, 3)))# Inspecting shapes of Y comparing reshaing methods
print(f'Y.shape: {Y.shape}')
print(f'Y.reshape: {tf.reshape(Y, (2, 3)).shape}')
print(f'Y.transpose: {tf.transpose(Y).shape}')# Check values of Y, reshape Y and tranposed Y
print("Y:")
print(Y, "\n") # "\n" for newline
print("Y reshaped to (2, 3):")
print(tf.reshape(Y, (2, 3)), "\n")
print("Y transposed:")
print(tf.transpose(Y))The different results could be explained:
tf.reshape()- change the shape of the given tensor (first) and then insert values in order they appear (in our case, 7, 8, 9, 10, 11, 12).tf.transpose()- swap the order of the axes, by default the last axis becomes the first, however the order can be changed using thepermparameter.
So which should you use?
Not Sure...
references, and examples
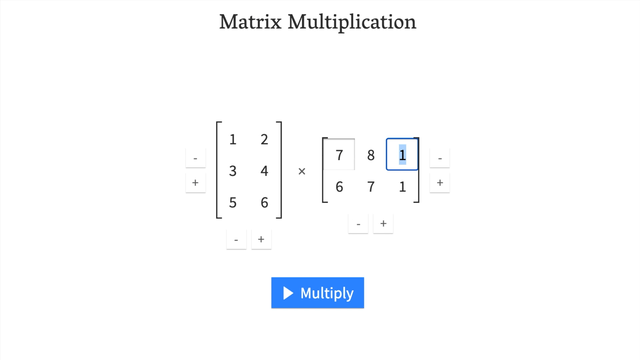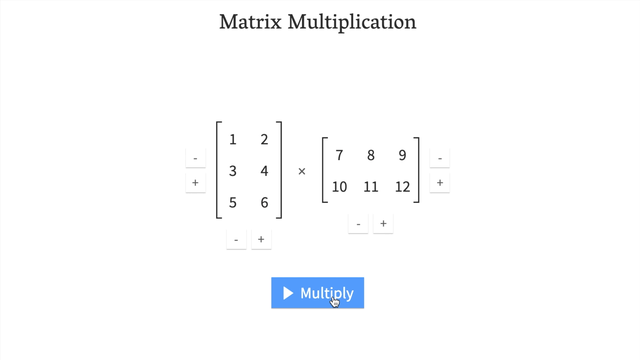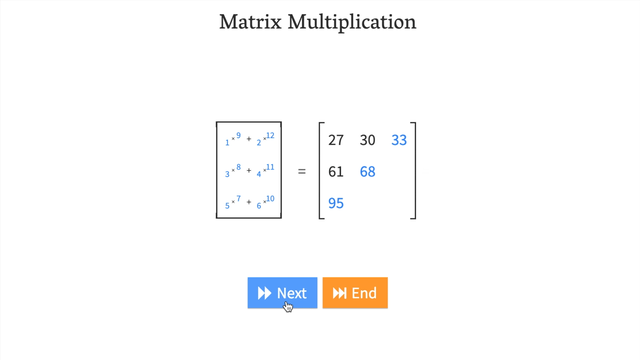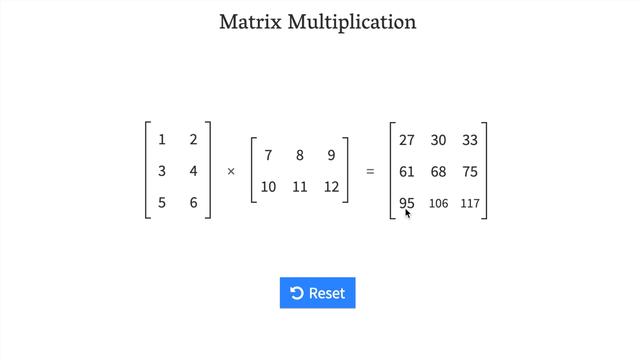
* If we transposedY, it would be represented as - Get an illustrative view of matrix multiplication by Math is Fun.
- Try a hands-on demo of matrix multiplcation: http://matrixmultiplication.xyz/ (shown below).
# Create tensor with negative values
D = tf.constant([-7, -10])
print(D)
# Get the absolute values
print(f'abs values: {tf.abs(D)}')Stats: min, max, mean, sum (aggregation)
To do so, aggregation methods typically have the syntaxreduce()_[action], such as:
tf.reduce_min()- find the minimum value in a tensor.tf.reduce_max()- find the maximum value in a tensor (helpful for when you want to find the highest prediction probability).tf.reduce_mean()- find the mean of all elements in a tensor.tf.reduce_sum()- find the sum of all elements in a tensor.
Also available are the standard deviation (tf.reduce_std()) and variance (tf.reduce_variance()).
Note: typically, each of these is under the math module, e.g. tf.math.reduce_min() but you can use the alias tf.reduce_min().
# Create a tensor with 50 random values between 0 and 100
E = tf.constant(np.random.randint(low=0, high=100, size=50))
print(E)
print('--------')
# minimum
print(f'MIN: {tf.reduce_min(E)}')
# maximum
print(f'MAX: {tf.reduce_max(E)}')
# mean
print(f'MEAN: {tf.reduce_mean(E)}')
print(f'SUM: {tf.reduce_sum(E)}')Finding the positional maximum and minimum
*tf.argmax() - find the position of the maximum element in a given tensor.
tf.argmin()- find the position of the minimum element in a given tensor.
# Create a tensor with 50 values between 0 and 1
F = tf.constant(np.random.random(50))
F# Find the maximum element position of F
tf.argmax(F)# Find the minimum element position of F
tf.argmin(F)# Find the maximum element position of F
print(f"The maximum value of F is {tf.reduce_max(F).numpy()} at position: {tf.argmax(F).numpy()}")
print(f"Using tf.argmax() to index F, the maximum value of F is: {F[tf.argmax(F)].numpy()}")
print(f"Are the two max values the same? {F[tf.argmax(F)].numpy() == tf.reduce_max(F).numpy()}")# Create a list of indices
some_list = [0, 1, 2, 3]
# One hot encode them
print(tf.one_hot(some_list, depth=len(some_list)))
print(tf.one_hot(some_list, depth=len(some_list) - 2))# Specify a custom one-hot values for on and off encoding
on="ON"
off="-"
tf.one_hot(some_list, depth=4, on_value=on, off_value=off)Squaring, log, square root
*tf.square() - get the square of every value in a tensor.
tf.sqrt()- get the squareroot of every value in a tensor (note: the elements need to be floats or this will error).tf.math.log()- get the natural log of every value in a tensor (elements need to floats).
# Create a new tensor
H = tf.constant(np.arange(1, 10))
print(H)
H#
# Square
#
tf.square(H)
#
# sqrt
#
# shows error
# tf.sqrt(H)
# InvalidArgumentError: Value for attr 'T' of int64 is not in the list of allowed values: bfloat16, half, float, double, complex64, complex128
# ; NodeDef: {{node Sqrt}}; Op<name=Sqrt; signature=x:T -> y:T; attr=T:type,allowed=[DT_BFLOAT16, DT_HALF, DT_FLOAT, DT_DOUBLE, DT_COMPLEX64, DT_COMPLEX128]> [Op:Sqrt]# Change H to float32
H = tf.cast(H, dtype=tf.float32)
H# Find the square root
tf.sqrt(H)#
# log (input also needs to be float)
#
tf.math.log(H)Manipulating tf.Variable tensors
Change tensors in-place with
.assign()- assign a different value to a particular index of a variable tensor.add_assign()- add to an existing value and reassign it at a particular index of a variable tensor
# Create a variable tensor
I = tf.Variable(np.arange(0, 5))
print('I:')
print(I)
#
# Assign the final value a new value of 50
#
print('I.assing...')
print(I.assign([0, 1, 2, 3, 50]))
# NOTE: no copy made, the "original" gets the update
print('I again')
print(I)
#
#
#
# Add 10 to every element in I
print('I.assign_add')
I.assign_add([10, 10, 10, 10, 10])Tensors and NumPy
Tensors can also be converted to NumPy arrays using:np.array()- pass a tensor to convert to an ndarray (NumPy's main datatype)tensor.numpy()- call on a tensor to convert to an ndarray
Doing this can be helpful: it makes tensors iterable & makes NumPy's methods available
# Create a tensor from a NumPy array
J = tf.constant(np.array([3., 7., 10.]))
print(f'J: {J}')
print(f'type of J: {type(J)}')
print(f'J.numpy: {J.numpy()}')
print(f'new type of J: {type(J.numpy())}')# Create a tensor from NumPy and from an array
numpy_J = tf.constant(np.array([3., 7., 10.])) # will be float64 (due to NumPy)
tensor_J = tf.constant([3., 7., 10.]) # will be float32 (due to being TensorFlow default)
numpy_J.dtype, tensor_J.dtypeUsing @tf.function
Python functions might have the decorator @tf.function. For reference, RealPython's guide on decorators. Decorators modify a function in one way or another.
In the @tf.function decorator case, it turns a Python function into a callable TensorFlow graph. Which is a fancy way of saying, if you've written your own Python function, and you decorate it with @tf.function, when you export your code (to potentially run on another device), TensorFlow will attempt to convert it into a fast(er) version of itself (by making it part of a computation graph).
For more on this, read the Better performnace with tf.function guide.
# Create a simple function
def timesTwoPlusY(x, y):
return x ** 2 + y
x = tf.constant(np.arange(0, 10))
print(f'x: {x}')
y = tf.constant(np.arange(10, 20))
print(f'y: {y}')
print(timesTwoPlusY(x, y))# Create the same function and decorate it with tf.function
@tf.function
def tf_function(x, y):
return x ** 2 + y
tf_function(x, y)print(tf.config.list_physical_devices('GPU'))If the above outputs an empty array (or nothing), it means you don't have access to a GPU (or at least TensorFlow can't find it).
If you're running in Google Colab, you can access a GPU by going to Runtime -> Change Runtime Type -> Select GPU.
Matrix Practice
1. Create a vector, scalar, matrix and tensor with (any) values using tf.constant() 2. Find the shape, rank and size of the tensors from 1 3. Create two tensors containing random values between 0 and 1 with shape [5, 300] 4. Multiply the two tensors from 3 using matrix multiplication 5. Multiply the two tensors from 3 using dot product 6. Create a tensor with random values between 0 and 1 with shape [224, 224, 3] 7. Find the min and max values of the tensor from 6 8. Created a tensor with random values of shape [1, 224, 224, 3] then squeeze it to change the shape to [224, 224, 3] 9. Create a tensor with shape [10] using any values, then find the matrix item index which has the maximum value 10. One-hot encode the tensor in 9# 1
vectorTest = tf.constant([2, 3])
matrixTest = matrix = tf.constant([[2, 3],[4, 5]])
scalarTest = tf.constant(2)# 2
print('#2')
print('vector props:')
print(f'shape: {vectorTest.shape}')
print(f'rank: {tf.rank(vectorTest)}')
print(f'size: {tf.size(vectorTest)}')
print('')
print('matrix props:')
print(f'shape: {matrix.shape}')
print(f'rank: {tf.rank(matrix)}')
print(f'size: {tf.size(matrix)}')
#3
print('')
print('#3: 2 random tensors')
random_1 = tf.random.Generator.from_seed(42) # set the seed for reproducibility
randomTestOne = tf.random.uniform(shape=[5,300], minval=0, maxval=1)
randomTestTwo = tf.random.uniform(shape=[5,300], minval=0, maxval=1)
print(randomTestOne)
print(randomTestTwo)
print('')
print('#4: matmul the 2 random tensors with matmul')
print(tf.matmul(randomTestOne, tf.transpose(randomTestTwo)))
print('')
print('#5: multiply using dotproduct')
print(tf.tensordot(tf.transpose(randomTestOne), randomTestTwo, axes=1))print('')
print('#6: random tensor with shape')
testSix = tf.random.uniform(shape=[224, 224, 3], minval=0, maxval=1)
print(testSix)print('')
print('#7: min & max of that tensor')
print(f'min: {tf.reduce_min(testSix)}')
print(f'max: {tf.reduce_max(testSix)}')print('')
print('#8: random tensor & squeeze')
testEight = tf.random.uniform(shape=[1, 224, 224, 3])
print(f'testEight shape:{testEight.shape}')
print(f'testEight SQUEEZED:{tf.squeeze(testEight).shape}')print('#9: create with shape and custom vals')
my_values = [1, 2, 10, 4, 5, 6, 7, 8, 9, 3]
testNine = tf.constant(my_values, shape=[10])
print(testNine)
#find the matrix item index which has the maximum value
max_index = tf.argmax(testNine).numpy()
print(f"Index of the largest number: {max_index}")print('#10: one-hot-encode #9')
print(tf.one_hot(testNine, depth=len(testNine)))